当x趋近于O时tanx的极限等于0。根据两个重要的极限之一lim(x→0)sinx/x=1,因此当x→0时sinx的极限与此时x的极限是相等的,因此lim(x→ 0)sinx=0。而cosx在x=0处是连续函数,因此lim(x→0)cosx=1。从而lim(x→0)tanx=lim(x→0)sinx/cosx=lim(x→0)sinx/lim(x→0)cosx=0/1=0。
当x趋近于0时tanx等于多少
原创 | 2022-12-31 21:37:27 |浏览:1.6万
猜你想问
-
 为什么当x趋于1时 lnx等于 等于0.因为当X趋近于一的时候。那么10的指数就趋近于0。因为10的0次幂等于1。如果设lnX等于a。则10的a次幂等于1。这里面In是指以10为底的常用对数。所以1的对数...
为什么当x趋于1时 lnx等于 等于0.因为当X趋近于一的时候。那么10的指数就趋近于0。因为10的0次幂等于1。如果设lnX等于a。则10的a次幂等于1。这里面In是指以10为底的常用对数。所以1的对数... -
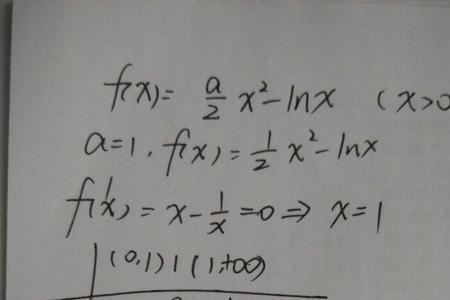 如何说明xlnx当x趋于0时极限值为0 lnx比x分之一,用洛必达法则求导。成1/x比负的x平方分之一。上下一约,成负的x.所以x趋于0为0x——>0时xlnx——>0,所以e的xlnx次方)减1,趋近于xlnx,你把xlnx看成u就...
如何说明xlnx当x趋于0时极限值为0 lnx比x分之一,用洛必达法则求导。成1/x比负的x平方分之一。上下一约,成负的x.所以x趋于0为0x——>0时xlnx——>0,所以e的xlnx次方)减1,趋近于xlnx,你把xlnx看成u就... -
 ipad能当xbox显示器用吗 可以。iPad可以当显示器使用。分别在电脑端和iPad下载安装【splashtop streamer】在电脑上打开该软件,点击【安全性】并设置安全密码在iPad打开该软件并选择需要连...
ipad能当xbox显示器用吗 可以。iPad可以当显示器使用。分别在电脑端和iPad下载安装【splashtop streamer】在电脑上打开该软件,点击【安全性】并设置安全密码在iPad打开该软件并选择需要连... -
 arcsinx当x=1时等于多少 答案:arcsinx当x=1时等于π/2具体解析:反三角正弦函数,定义域取值是在-1~1之间 ,对应此时的反三角函数的取值为负二分之派到二分之派之间,也就是x等于一时对应的反正...
arcsinx当x=1时等于多少 答案:arcsinx当x=1时等于π/2具体解析:反三角正弦函数,定义域取值是在-1~1之间 ,对应此时的反三角函数的取值为负二分之派到二分之派之间,也就是x等于一时对应的反正... -
 x/sinx当x趋向于无穷时极限为多少 x/sinx,当x趋向无穷时极限不存在,或者说发散于无穷大。对于x/sinx,我们都熟悉lim(x→0)ⅹ/sinx=1。但对于ⅹ趋向于无穷时lim(x→∞)x/sinx是多少呢因为对于sinx,它的...
x/sinx当x趋向于无穷时极限为多少 x/sinx,当x趋向无穷时极限不存在,或者说发散于无穷大。对于x/sinx,我们都熟悉lim(x→0)ⅹ/sinx=1。但对于ⅹ趋向于无穷时lim(x→∞)x/sinx是多少呢因为对于sinx,它的...
