没有这种说法。两个数可以互为质数,也可以有公因数。但不能说互为因数。如果互为质数,即这两个数只有一个因数是1。而1在实际运算中是不作为因数的,也就可以说互为质数是没有因数的。同时,两个不相同的质数一定是互质。只少有一个合数,那公这两个数就有可能出现公因数,公因数是两个或多个数申相同的质因数,公因数可以有一个,也可以有多个。

互质因数是什么意思
原创 | 2022-12-17 14:24:11 |浏览:1.6万
猜你想问
-
 什么叫两两不互质 两两不互质是说任意两个数不互质,有大于一的公约数,原始凭证有错误的,应当由出具单位重开或更正,更正处应当加盖出具单位印章。原始凭证金额有错误的,应当由出具单位重...
什么叫两两不互质 两两不互质是说任意两个数不互质,有大于一的公约数,原始凭证有错误的,应当由出具单位重开或更正,更正处应当加盖出具单位印章。原始凭证金额有错误的,应当由出具单位重... -
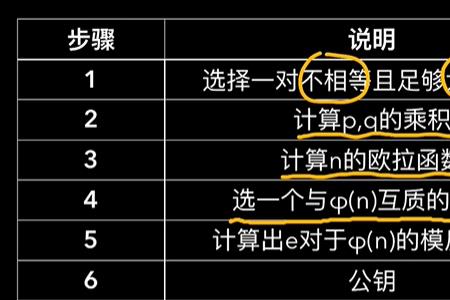 为什么p q是互质的整数 pq是互质的整数有道理。互质数是指公约数只有1的两个整数,叫做互质数。如1和(零除外)的任何整数都是互质数。两个质数也是互质数。任意相邻的两个整数(零除外)也是互质...
为什么p q是互质的整数 pq是互质的整数有道理。互质数是指公约数只有1的两个整数,叫做互质数。如1和(零除外)的任何整数都是互质数。两个质数也是互质数。任意相邻的两个整数(零除外)也是互质... -
 mn互质整数什么意思 两个数互质就是指这两个数的公因数只有1的两个非零自然数,叫做互质数。举例:2和3,公因数只有1,为互质数。        对m和n进行因数分解,当m和n的最大公...
mn互质整数什么意思 两个数互质就是指这两个数的公因数只有1的两个非零自然数,叫做互质数。举例:2和3,公因数只有1,为互质数。        对m和n进行因数分解,当m和n的最大公... -
 互质数怎么通分 这道题目后门或者是怎么去通生,就比如1/2和1/4,他们身为互质数,然后通分的话,我们要找它们的最小公倍数,最小公倍数为六的话,我们2~6的话要陈三,所以我们分子分母同时乘...
互质数怎么通分 这道题目后门或者是怎么去通生,就比如1/2和1/4,他们身为互质数,然后通分的话,我们要找它们的最小公倍数,最小公倍数为六的话,我们2~6的话要陈三,所以我们分子分母同时乘... -
 什么叫做m,n互质 解m,n互质就m与n这两个数的最大公约数只有1。m,n这两个可以有一个是质数,一个是合数。也可能两个数都是质数,也可两个都是合数。它们的最小公倍数是m与n的乘积。举例...
什么叫做m,n互质 解m,n互质就m与n这两个数的最大公约数只有1。m,n这两个可以有一个是质数,一个是合数。也可能两个数都是质数,也可两个都是合数。它们的最小公倍数是m与n的乘积。举例...
