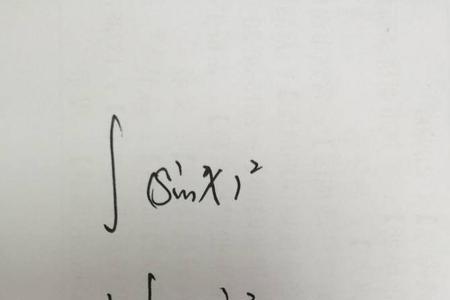∫cosx的平方dx等于x乘以1/2加上sin2x乘以1/4加上常数C,理由如下:被积式cosx的平方等于二分之一加上cos2x乘以二分之一的积,则∫1/2dx=x乘以1/2+常数,∫cos2xdx=1/2*∫cos2xd2x=1/2*sin2x加上常数,由积分运算性质,得的结果为1/2*x+1/4*sin2x+C.
∫cos²xdx等于多少
∫cos²xdx=∫[(cos2x+1)/2]dx=(1/2)[∫cos2xdx+∫dx]=(1/2)[(1/2)sin2x+x]+c=(1/4)sin2x+(1/2)x+cc任意常数