对角线乘积的一半是谁的面积

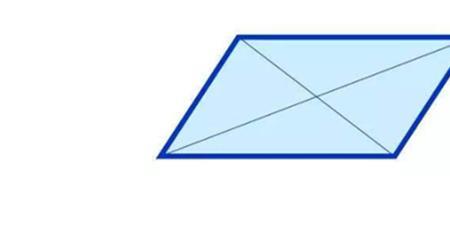
是菱形和正方形的面积

证明：设菱形ABCD，其对角线AC与BD相交于O点。根据菱形的性质AC与BD垂直。BO是△ABC的底边AC上的高，△ABC的面积

S=AC×BO/2，同理△ACD的面积

S=AC×DO/2。

菱形ABCD的面积S=△ABC与△CDA的面积之和=AC×BO/2+AC×DO/2

=AC×(BO+DO)/2

=AC×BD/2

证明完毕。正方形是菱形的一种。菱形是四边相等的平行四边形，正方形是相邻边互相垂直的菱形。

对角线乘积的一半是谁的面积

1、对角线乘积的一半是对角线互相垂直的四边形的面积。

证明：

设该四边形为ABCD，AC与BD为互相垂直的对角线，且AC与BD的交点为O。

因为AC*BD=（AO+CO）BD=AO*BD+CO*BD=2*[(AO*BD)/2+(CO*BD)/2]

又因为三角形ABD面积为BD*AO/2

三角形BCD面积为BD*CO/2

所以对角线互相垂直的四边形的面积等于对角线乘积的一半。

2、对角线垂直的四边形有特性：

特性一：它的面积等于两条对角线长的乘积的一半。

特性二：连接四条的中点所形成的四边形是矩形。

特性三：由对角线相交所得的四条线段的平方和等于四边形四条边的平方和的一半

对角线乘积的一半是谁的面积

对角线乘积的一半是正方形的面积，说明如下：假设正方形边长为a，则对角线长度为√2×a，对角线乘积为2a²，对角线乘积的一半为a²即正方形的面积