倾斜角tan的范围

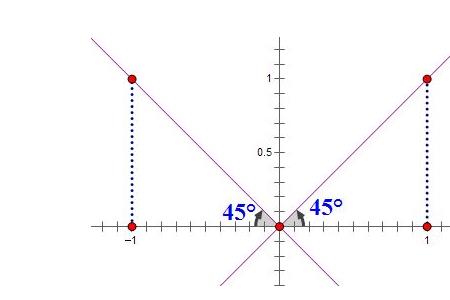
0°≤α<180°(α≠90°)。平面直角坐标系内，当直线l与x轴相交时，我们取x轴作为基准，x轴正向与直线l向上方向之间所成的角a叫做直线l的倾斜角。倾斜角不是90°的直线，它的倾斜角的正切值叫做这条直线的斜率。直线的斜率常用k表示，与y轴重合的直线无斜率。

倾斜角的取值范围

倾斜角公式

k=tanα

k>0时α∈（0°，90°）

k<0时α∈（90°，180°）

k=0时α=0°

当α=90°时k不存在

ax+by+c=0(a≠0）倾斜角为A

则tanA=-a/b

A=arctan(-a/b)

当a≠0时

倾斜角为90度，即与X轴垂直

倾斜角tan的范围

（1）直线l的倾斜角α≠90°时，正切值tanα存在，此时斜率k=tanα。

（2）直线l的倾斜角α=90°时，正切值tanα不存在，此时斜率k也不存在。

（3）两直线的斜率相等，则它们的倾斜角相等两直线的斜率不相等，则它们的倾斜角也不相等。

（4）两直线的倾斜角不相等，则它们的斜率也一定不相等两直线的倾斜角相等，则它们的斜率要么存在且相等，要么都不存在。

一、直线的倾斜角

1、平面直角坐标系中，规定直线与x轴平行或重合时的倾斜角为0°。

2、平面直角坐标系中，直线不与x轴平行或重合时必与x轴相交。此时，以x轴为基准，x轴正向与直线向上的方向之间所成的角叫作直线的倾斜角。

直线与其倾斜角示意图

【注】直线倾斜角α的取值范围为：0°≤α<180°。

二、直线的斜率

1、当直线倾斜角不等于90°时，常用一条直线的斜率k来刻画这条直线的倾斜程度。定义直线斜率k等于直线倾斜角α的正切值，即k=tanα.

2、特别地，对于正比例函数y=kx(k≠0)和一次函数y=kx+b(k≠0)来说，x的系数k就是正比例函数y=kx和一次函数y=kx+b所对应的直线的斜率。

三、直线斜率与倾斜角的关系

1、直线l的倾斜角α≠90°时，正切值tanα存在，此时斜率k=tanα。

2、直线l的倾斜角α=90°时，正切值tanα不存在，此时斜率k也不存在。

3、两直线的斜率相等，则它们的倾斜角也相等两直线的斜率不相等，则它们的倾斜角也不相等。

4、两直线的倾斜角不相等，则它们的斜率也一定不相等两直线的倾斜角相等，则它们的斜率要么存在且相等，要么都不存在。

5、当直线倾斜角α从0°增大到90°时，斜率k从0增大到“正无穷大”。即α∈[0°，90°)时，k∈[0，+∞)。

6、当直线倾斜角α从90°增大到180°时，斜率k从“负无穷大”增大到0。即α∈(90°，180°)时，k∈(-∞，0)。

倾斜角tan的范围

直线倾斜角α∈[0，兀），任何直线都有倾斜角。而倾斜角正切值是直线斜率，即k＝tanα（α≠兀／2），并不是所有直线都有斜率。由于倾斜角范围并不是正切函数单调区间。所以求两者范围转化时需确定区间，仔细讨论