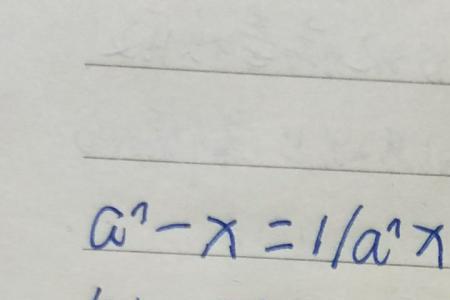按照乘方的定义:n个相同的数的乘积叫做这个数的n次幂或叫做n次乖方。零当然也包括其中。零的n次幂就是n个零相乘。但这里的n是正整数。
当指数概念扩大化后,就出现了零指数,分数指数,负指数等。零指数是两个同底同指数的幂相除,指数相减出现的。按照相同的两个数相除商为1,当然要规定零次幂等于1。但零不能当除数,所以零的零次幂无意义。
所以零次幂的底数的取值范围是不等于零的数。
零次幂的底数取值范围
零指数幂底数的取值范围:底数不能为0。
一般地,在数学上我们把ⁿ个相同的因数a相乘的积记做a^ⁿ。这种求几个相同因数的积的运算叫做乘方,乘方的结果叫做幂。在a^ⁿ中,a叫做底数,ⁿ叫做指数。a^ⁿ读作“a的ⁿ次方”或“a的ⁿ次幂“。
零指数幂指的是零指数幂法则。零指数幂法则:任何一个不等于零的数的零次幂都等于1。
扩展资料
正整数指数幂的运算性质如下:
(1)aᵐ·aⁿ=aᵐ+ⁿ(m,n是正整数).
(2)(aᵐ)ⁿ=aᵐⁿ(m,n是正整数)
(3)(ab)ⁿ=aⁿbⁿ(n是正整数)
4)aᵐ÷aⁿ=aᵐ-ⁿ(a≠0,m,n是正整数,m>n)
(5)a⁰=1(a≠0)