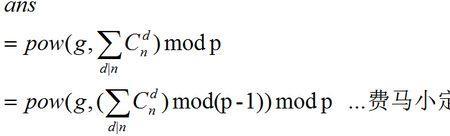高斯-卢卡斯定理,又称卢卡斯定理,该定理描述了复系数多项式的一个性质:多项式导数的根一定在原多项式的根所构成的凸包内。
这一结论曾在1836被Carl Friedrich Gauss直接使用,1874 得到证明。
Lucas定理是同余理论中的一个很重要的定理,用于组合数取模。常常使用在问题的结果需要对某个数据取模,n,m很大,达到1e15以上,但是p在1e9以内。一般来说最好的效果实在1e5以内。
lucas定理
Lucas定理是用来求 c(n,m) mod p,p为素数的值。
中文名:卢卡斯定理
外文名:Lucas' Theorem
表达式:C(n,m)%p=C(n/p,m/p)*C(n%p,m%p)%p
提出者:卢卡斯
适用领域:数论(较大的组合数对素数p求模)
应用学科:数学、信息学
定律定义:
Lucas定理:我们令n=sp+q , m=tp+r .(0≤q ,r ≤p-1)
那么:(在编程时你只要继续对 调用Lucas定理即可。
代码可以递归的去完成这个过程,其中递归终点为t = 0
时间O(logp(n)*p):)