函数y=arctanx是一个奇函数。具体原因如下:笫一,它的定义域为R,即(一∞,十∞),这是一个关于原点0对称的区间,滿足函数具有奇偶性的必要条件。笫二,如果θ=arctanx,那么根据正切函数的性质正切等于一x的且在(一π/2,π/2)内的角只能是一θ,即一arctanx,故arctan(一x)=-arctanx。
arctan函数的奇偶性
原创 | 2022-11-19 10:30:27 |浏览:1.6万
猜你想问
-
 rare造句 His chances of meeting dorothea were rare .他跟多萝西娅见面的机会极少。Both-handed tennis players are rare .能用左右手打网球的人很少。A top hat is a r...
rare造句 His chances of meeting dorothea were rare .他跟多萝西娅见面的机会极少。Both-handed tennis players are rare .能用左右手打网球的人很少。A top hat is a r... -
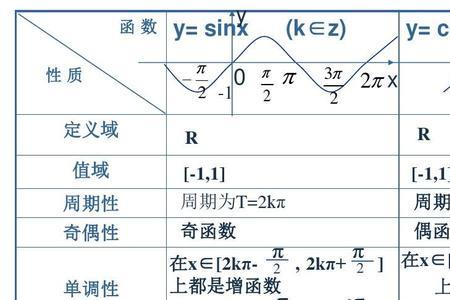
 3dmark压力测试多少不及格 3dmark压力测试3%不及格最终显卡以99.4%的成绩通过测试,说明显卡的稳定性是没有问题的。3dmark压力测试能测试出电脑的整体性能水平,特别是显卡的性知能,3dmark压力...
3dmark压力测试多少不及格 3dmark压力测试3%不及格最终显卡以99.4%的成绩通过测试,说明显卡的稳定性是没有问题的。3dmark压力测试能测试出电脑的整体性能水平,特别是显卡的性知能,3dmark压力... -
 压力测试3dmark要测多久出结果 10分钟左右3dmark压力测试能测试出电脑的整体性能水平,特别是显卡的性能,3dmark压力测试一般循环20次,耗时10分钟左右...
压力测试3dmark要测多久出结果 10分钟左右3dmark压力测试能测试出电脑的整体性能水平,特别是显卡的性能,3dmark压力测试一般循环20次,耗时10分钟左右... -
 arctan√x等于什么 arctanVx并不会直接等于什么一个具体的实数,它的具体答案的数值是与x的大小有关的,但我们可以确定它的取值范围在[0,π/4)之内。我们知道arctanx的主值范围是(-π/2,...
arctan√x等于什么 arctanVx并不会直接等于什么一个具体的实数,它的具体答案的数值是与x的大小有关的,但我们可以确定它的取值范围在[0,π/4)之内。我们知道arctanx的主值范围是(-π/2,... -
 secarctan等于多少 正割函数和余弦函数互为倒数。即: secx=1/cosx。arctanx是反正切函数。用直角三角形来推导。设直角三角形ABC中∠C为直角其所对的边为斜边c,两个锐角为∠A和∠B所对...
secarctan等于多少 正割函数和余弦函数互为倒数。即: secx=1/cosx。arctanx是反正切函数。用直角三角形来推导。设直角三角形ABC中∠C为直角其所对的边为斜边c,两个锐角为∠A和∠B所对...
