正弦函数怎样化成一般式

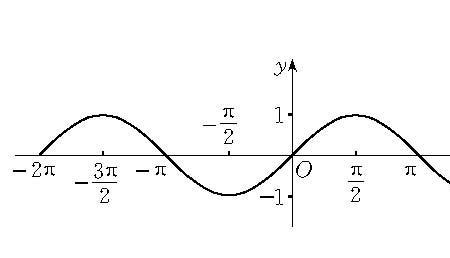
正弦函数一般解析式：f(x)= Asin(ωx+φ)+h， |A|≠0， |ω|≠0 定义域：实数集R

值域公式：[-|A|+h ，|A|+h]

周期公式：2π/|ω|

奇偶性：奇函数

对称轴公式：

直线x=(π/2−φ+kπ)/ω，k∈Z

对称中心公式:((-φ+ kπ)/ω，h)，k∈Z

我们要灵活运用三角恒等变换，无论是展开还是合并，都是为了更好地将题目化简，更容易地分析出我们想要获得的结论。

正弦函数怎样化成一般式

举个例子先y=(sinx+cosx)^2+2cos^2x

=sin^2x+2sinxcosx+cos^2x+2cos^2x

=1+sin2x+2cos^2x

=1+sin2x+2*(1+cos2x)2

=1+sin2x+1+cos2x

=2+√2sin(2x+45°) 因为sin(A+B)＋sin(A-B)

＝(sinAcosB+cosAsinB)＋(sinAcosB-cosAsinB)

＝2sinAcosB

所以sinAcosB＝(1/2)[sin(A+B)＋sin(A-B)]

上面这个叫做积化和差公式，类似可以得到cosAsinB，cosAcosB，sinAsinB的公式 3