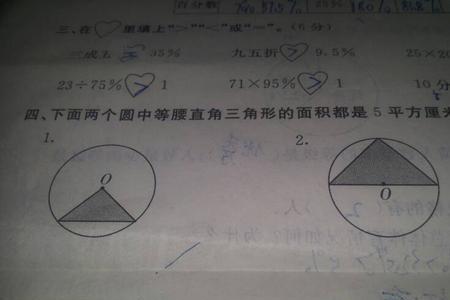
圆内接三角形面积最大时是正三角形。证明过程:
设三角形duABC外接圆半径为r,则
S三角形ABC
=(1/2)absinC
=2r^dao2sinAsinBsinC
<=2r^2[(sinA+sinB+sinC)/3]^3(均值不等回式)答
<=2r^2{sin[(A+B+C)/3]}^3=(3√3/4)r^2(琴生不等式)
等号当sinA=sinB=sinC,即A=B=C时成立,所以当三角形为正三角形时面积最大。
原创 | 2022-11-17 19:06:57 |浏览:1.6万
圆内接三角形面积最大时是正三角形。证明过程:
设三角形duABC外接圆半径为r,则
S三角形ABC
=(1/2)absinC
=2r^dao2sinAsinBsinC
<=2r^2[(sinA+sinB+sinC)/3]^3(均值不等回式)答
<=2r^2{sin[(A+B+C)/3]}^3=(3√3/4)r^2(琴生不等式)
等号当sinA=sinB=sinC,即A=B=C时成立,所以当三角形为正三角形时面积最大。




Copyright 2005-2020 www.kxting.com 版权所有 |  湘ICP备2023022655号
湘ICP备2023022655号
声明: 本站所有内容均只可用于学习参考,信息与图片素材来源于互联网,如内容侵权与违规,请与本站联系,将在三个工作日内处理,联系邮箱:47085,1089@qq.com