矩阵不可逆有什么性质

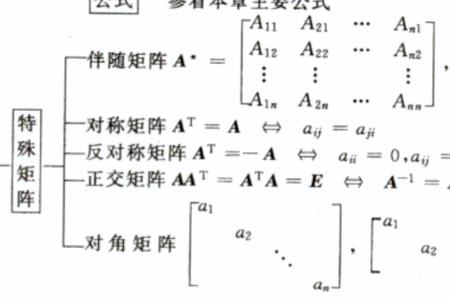
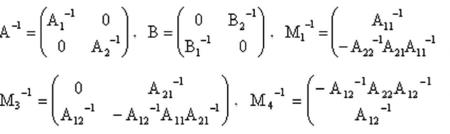不可逆矩阵的特点：

|A| = 0A的列（行）向量组线性相关R(A)<nAX=0 有非零解A有特征值0A不能表示成初等矩阵的乘积A的等价标准形不是单位矩阵。

元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。

矩阵的性质：

在线性代数中，三角矩阵是方形矩阵的一种，因其非零系数的排列呈三角形状而得名。三角矩阵分上三角矩阵和下三角矩阵两种。

在线性代数中，相似矩阵是指存在相似关系的矩阵。相似关系是两个矩阵之间的一种等价关系。两个n×n矩阵A与B为相似矩阵当且仅当存在一个n×n的可逆矩阵P。

矩阵不可逆有什么性质

奇异矩阵不可逆，即矩阵的行列式为0(或者说矩阵不满秩）的时候，则矩阵A不可逆。奇异矩阵是线性代数的概念，就是对应的行列式等于0的方阵。如果A为奇异矩阵，则AX=0有无穷解，AX=b有无穷解或者无解。