向量斯坦纳定理最简证明方法

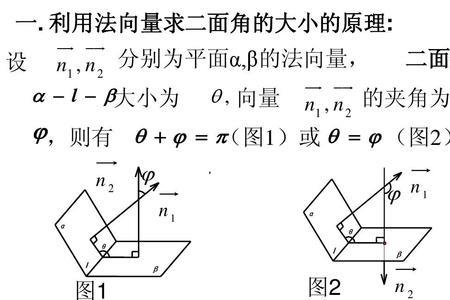
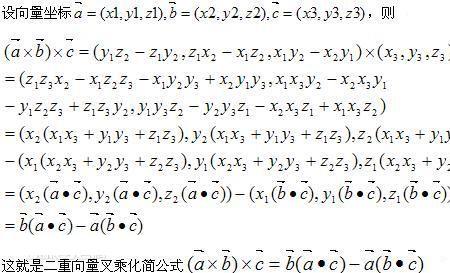斯坦纳-雷米欧司定理:

设在三角形ABC中，有B、C的角平分线CF、BE交于O

BE是角平分线推出：BC/CE=AB/AE，同理：BC/BD=AC/AD，因为BD=CE，所以等量代换得出：

AB/AE=AC/AD，角A是公共角，所以三角形ACD与ABE相似，所以LACD=LABE，同理LBDC=LBEC，再加上BD=CE，所以三角形BOD全等于三角形OEC，所以OB=OC且LDBE=LECD，OB=OC推出LOBC=LOCB，再等量代换得到LABC=LACB，所以AB=AC

向量斯坦纳定理最简证明方法

在△ABC中，BD，CE为其角平分线，且BD=CE

设∠ABD=∠CBD=x，∠ACE=∠BCE=y

根据张角定理，有

2cosx/BD=1/AB+1/BC

2cosy/CE=1/AC+1/BC

则2*AB*BC*cosx/(AB+BC)=BD=CE=2*AC*BC*cosy/(AC+BC)

即(AB*(AC+BC))/(AC*(AB+BC))=cosy/cosx

利用分比定理。并对cosy-cosx使用和差化积

AB-AC=(-(2*AC*(AB+BC))/(BC*cosx))*sin((y+x)/2)*sin((y-x)/2)

若AB>AC，则上式左端为正，右端为负

若AB<AC，则上式左端为负，右端为正

故AB=AC

斯坦纳-雷米欧司定理: 设在三角形abc中，有b、c的角平分线cf、be交于o be是角平分线推出：bc/ce=ab/ae，同理：bc/bd=ac/ad，因为bd=ce，所以等量代换得出： ab/ae=ac/ad，角a是公共角，所以三角形acd与abe相似，所以lacd=labe，同理lbdc=lbec，再加上bd=ce，所以三角形bod全等于三角形oec，所以ob=oc且ldbe=lecd，ob=oc推出lobc=locb，再等量代换得到labc=lacb，所以ab=ac 注:"l"为角的符号